Variance là gì? Khám phá khái niệm quan trọng trong thống kê và tài chính

Variance (phương sai) là một khái niệm quan trọng trong thống kê và tài chính, giúp đo lường mức độ biến đổi của dữ liệu. Nó thường được sử dụng để đánh giá sự phân tán và đo lường độ biến thiên của các giá trị trong một tập dữ liệu. Trong bài viết này, chúng ta sẽ tìm hiểu về định nghĩa variance là gì, vai trò của variance, cùng với cách tính toán và ứng dụng thực tế của nó trong lĩnh vực thống kê và tài chính.

Hãy cùng với góc nghề nghiệp đi sâu vào khám phá khái niệm quan trọng này để hiểu rõ hơn về sự biến đổi của dữ liệu và tầm quan trọng của nó trong các phân tích và quyết định kinh doanh nhé.

Variance là gì?

Định nghĩa variance

Variance là một khái niệm trong thống kê và tài chính được sử dụng để đo lường mức độ biến đổi của dữ liệu trong một tập hợp. Nó thể hiện mức độ đánh rơi giữa các giá trị dữ liệu so với giá trị trung bình. Khi chỉ số variance càng lớn, có nghĩa là dữ liệu có sự biến đổi lớn, trong khi khi variance nhỏ hơn thì dữ liệu có sự tập trung và ổn định hơn.

Ý nghĩa và vai trò của variance trong thống kê và tài chính

• Đánh giá sự biến đổi dữ liệu: Variance cho phép đánh giá mức độ biến thiên của dữ liệu trong một tập hợp. Khi thực hiện phân tích dữ liệu, việc biết đến mức độ biến đổi này giúp ta hiểu rõ hơn về tính chất và đặc điểm của dữ liệu, từ đó đưa ra những kết luận và quyết định phù hợp.
• Đo lường độ biến thiên: Phương sai cũng là một phương tiện quan trọng để đo lường độ biến thiên giữa các tập dữ liệu khác nhau. Điều này hỗ trợ trong việc so sánh và lựa chọn các tập dữ liệu có tính chất gần giống nhau hoặc ổn định để tiến hành các phân tích hay quyết định kinh doanh.
• Quản lý rủi ro trong tài chính: Trong lĩnh vực tài chính, variance đóng vai trò quan trọng trong việc đo lường và quản lý rủi ro. Khi đầu tư hoặc làm việc với tài sản tài chính, hiểu rõ mức độ biến đổi của chúng giúp đánh giá nguy cơ và lợi ích, từ đó đưa ra quyết định đầu tư hiệu quả.

Tóm lại, phương sai là một khái niệm quan trọng trong thống kê và tài chính, giúp đo lường và đánh giá mức độ biến đổi của dữ liệu. Việc hiểu rõ và ứng dụng phương sai một cách hợp lý trong các phân tích và quyết định kinh doanh là một yếu tố cơ bản để đạt được hiệu quả và thành công trong lĩnh vực này.

Xem thêm: Business Model là gì? Ý nghĩa và Tầm quan trọng trong kinh doanh

Cách tính toán variance

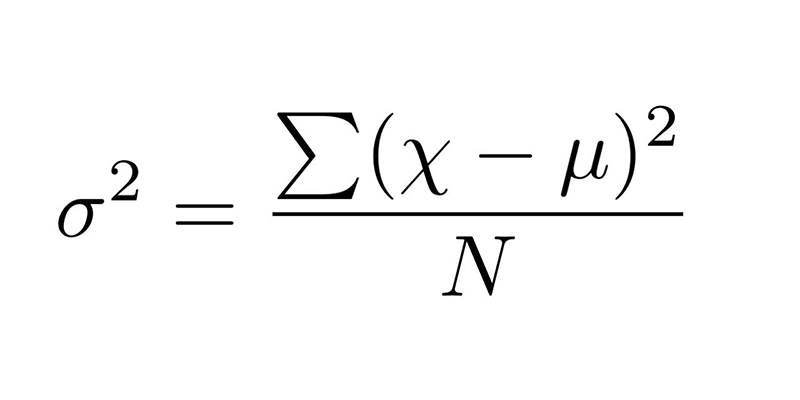
Công thức tính toán variance

Variance là một phương pháp đo lường sự biến đổi của dữ liệu từ giá trị trung bình. Để tính toán variance, ta làm như sau:

• Tính giá trị trung bình của dữ liệu (mean, μ).
• Tính bình phương của độ sai lệch của từng giá trị so với giá trị trung bình.
• Tổng hợp các bình phương sai lệch và chia cho số lượng giá trị trong tập dữ liệu (n).

Công thức tính variance (σ^2) như sau:

• σ^2 = Σ (xi – μ)^2 / n

Trong đó: σ^2 là phương sai Σ là ký hiệu tổng hợp, tức là tính tổng của tất cả các thành phần trong ngoặc. xi là từng giá trị trong tập dữ liệu μ là giá trị trung bình của tập dữ liệu n là số lượng giá trị trong tập dữ liệu.

Ví dụ minh họa cách tính variance

Giả sử chúng ta có tập dữ liệu sau đây đại diện cho số lượng sản phẩm bán ra hàng tháng trong 6 tháng liên tiếp: 50, 60, 45, 55, 65, 50.

• Bước 1: Tính giá trị trung bình (μ): μ = (50 + 60 + 45 + 55 + 65 + 50) / 6 = 51.67
• Bước 2: Tính bình phương của độ sai lệch của từng giá trị so với giá trị trung bình: (50 – 51.67)^2 ≈ 2.78 (60 – 51.67)^2 ≈ 70.22 (45 – 51.67)^2 ≈ 44.56 (55 – 51.67)^2 ≈ 11.22 (65 – 51.67)^2 ≈ 179.78 (50 – 51.67)^2 ≈ 2.78
• Bước 3: Tính tổng hợp các bình phương sai lệch và chia cho số lượng giá trị trong tập dữ liệu (n): σ^2 = (2.78 + 70.22 + 44.56 + 11.22 + 179.78 + 2.78) / 6 ≈ 54.11
• Variance của tập dữ liệu là khoảng 54.11.

Đây là cách tính toán phương sai từ tập dữ liệu cho trước. Phương sai giúp chúng ta hiểu rõ hơn về sự biến đổi và phân tán của dữ liệu, từ đó thực hiện các phân tích và quyết định hiệu quả trong lĩnh vực thống kê và tài chính.

Xem thêm: Quy luật kinh tế là gì? Tìm hiểu khái niệm cơ bản và ý nghĩa

Ứng dụng của variance

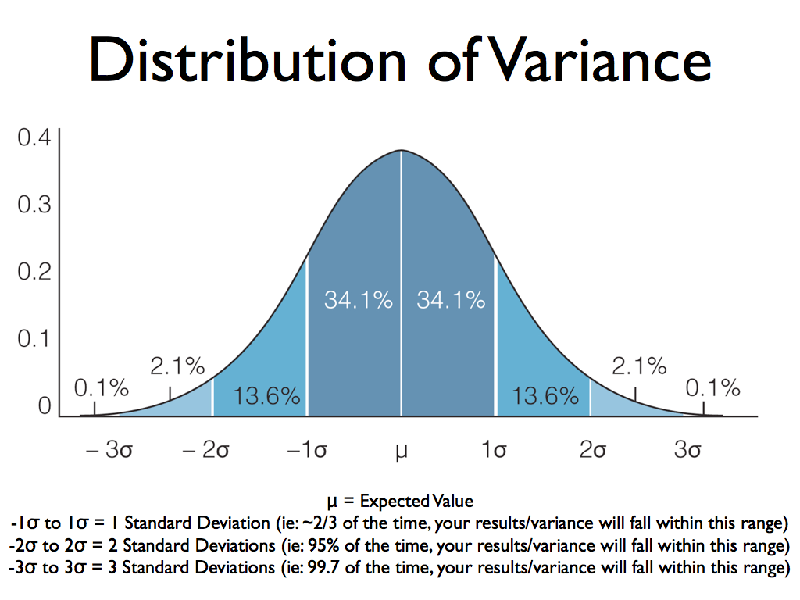
Variance trong thống kê

• Đánh giá sự phân tán và biến đổi dữ liệu: Variance giúp đo lường mức độ phân tán và biến đổi của dữ liệu trong một tập hợp. Khi phương sai lớn, có nghĩa là dữ liệu có sự biến đổi mạnh, trong khi phương sai nhỏ hơn thể hiện dữ liệu tập trung và ổn định hơn. Điều này giúp nhận diện các xu hướng, biến đổi và khả năng dự đoán kết quả của dữ liệu.
• Ước lượng sai số và độ tin cậy của mẫu: Variance là một trong các thành phần quan trọng trong việc ước lượng sai số và độ tin cậy của mẫu. Nó được sử dụng trong các phương pháp thống kê để đo lường sự biến đổi giữa các mẫu, từ đó xác định mức độ chính xác và đáng tin cậy của kết quả thống kê.

Variance trong tài chính

• Ứng dụng trong quản lý rủi ro đầu tư: Trong lĩnh vực tài chính, quản lý rủi ro là một yếu tố quan trọng đối với các nhà đầu tư. Variance được sử dụng để đo lường rủi ro của các tài sản tài chính và đánh giá khả năng biến động của giá cổ phiếu, tiền tệ, hay tài sản khác. Việc hiểu rõ rủi ro giúp nhà đầu tư đưa ra các quyết định đầu tư hợp lý và tối ưu hóa lợi nhuận.
• Đánh giá hiệu quả các chiến lược đầu tư: Các chiến lược đầu tư thường liên quan đến việc định giá tài sản, dự đoán xu hướng thị trường và tối ưu hóa lợi nhuận. Phương sai được sử dụng để đánh giá hiệu quả của các chiến lược này, từ đó giúp nhà đầu tư xác định các kế hoạch đầu tư tốt nhất và tránh những rủi ro không đáng giá.

So sánh variance với các khái niệm liên quan

So sánh variance với standard deviation

• Định nghĩa:
  • Variance là đo lường độ biến đổi của dữ liệu dựa trên bình phương sai số giữa từng giá trị và giá trị trung bình của tập dữ liệu.
  • Standard deviation (độ lệch chuẩn) là căn bậc hai của variance, thể hiện mức độ biến đổi của dữ liệu theo đơn vị gốc (đơn vị đo lường) của dữ liệu.
• Biểu diễn:
  • Variance được ký hiệu bằng σ^2.
  • Standard deviation được ký hiệu bằng σ.
• Tính toán:
  • Variance được tính bằng cách tính tổng bình phương sai số của từng giá trị so với giá trị trung bình và chia cho số lượng giá trị trong tập dữ liệu.
  • Standard deviation được tính bằng căn bậc hai của phương sai.
• Ưu điểm và nhược điểm:
  • Variance có ưu điểm là nó bao gồm tất cả các giá trị dữ liệu và đo lường độ biến đổi mạnh hơn. Tuy nhiên, do được tính bằng bình phương của sai số, nó có thể làm tăng độ lớn của các giá trị và khó hiểu trong việc so sánh giữa các tập dữ liệu khác nhau.
  • Standard deviation giữ nguyên đơn vị đo lường ban đầu, giúp dễ dàng so sánh độ biến đổi giữa các tập dữ liệu và dễ hiểu hơn. Nhược điểm là nó không nhấn mạnh đến những giá trị ngoại lai (outliers).

So sánh variance và covariance

• Định nghĩa:
  • Phương sai là đo lường mức độ biến đổi của một biến đơn lẻ trong một tập dữ liệu.
  • Covariance là đo lường mức độ biến đổi chung giữa hai biến trong một tập dữ liệu.
• Biểu diễn:
  • Variance được ký hiệu bằng σ^2.
  • Covariance được ký hiệu bằng Cov(X, Y) hoặc σ(X, Y).
• Tính toán:
  • Variance tính bằng cách tính tổng bình phương sai số của từng giá trị so với giá trị trung bình và chia cho số lượng giá trị trong tập dữ liệu.
  • Covariance tính bằng cách tính tổng tích chất của độ sai lệch của từng cặp giá trị X và Y so với giá trị trung bình của X và Y và chia cho số lượng giá trị trong tập dữ liệu.
• Ý nghĩa:
  • Variance tập trung vào sự biến đổi của một biến đơn lẻ.
  • Covariance tập trung vào mối quan hệ tương quan giữa hai biến.

Tóm lại, phương sai và standard deviation đo lường mức độ biến đổi của dữ liệu, nhưng có điểm khác nhau về đơn vị đo lường và cách tính toán. Trong khi đó, covariance đo lường mối quan hệ tương quan giữa hai biến. Việc hiểu rõ và sử dụng các khái niệm này giúp chúng ta phân tích dữ liệu và quản lý rủi ro hiệu quả trong nhiều lĩnh vực, từ thống kê đến tài chính.

Những thách thức khi sử dụng variance

Ảnh hưởng của dữ liệu ngoại lai (outliers) đối với variance

Dữ liệu ngoại lai (outliers) là các giá trị cực kỳ khác biệt với phần còn lại của tập dữ liệu. Khi có dữ liệu ngoại lai trong tập dữ liệu, phương sai có thể bị ảnh hưởng mạnh, dẫn đến việc bị sai lệch và không phản ánh chính xác mức độ biến đổi của dữ liệu chung.

Ví dụ: Giả sử chúng ta có tập dữ liệu chiều cao của một nhóm người, và trong đó có một người cao hơn rất nhiều so với những người khác. Nếu không loại bỏ dữ liệu ngoại lai này, phương sai sẽ cao hơn nhiều so với trường hợp loại bỏ, dẫn đến việc đánh giá sai về mức độ biến đổi của chiều cao trong nhóm người này.

Rủi ro sai tưởng khi không hiểu rõ giá trị variance

Phương sai là một chỉ số đo lường độ biến đổi của dữ liệu và nó có thể dẫn đến những rủi ro sai tưởng khi không được hiểu rõ và đánh giá chính xác. Một số rủi ro khi sử dụng variance là:

• Hiểu sai về đơn vị đo lường: Phương sai được tính bằng bình phương của sai số và do đó có đơn vị đo lường là bình phương của đơn vị gốc. Khi không nhận ra điều này, người sử dụng có thể hiểu sai về mức độ biến đổi thực sự của dữ liệu.
• Không đánh giá cẩn thận các giá trị ngoại lai: Như đã đề cập ở trên, dữ liệu ngoại lai có thể ảnh hưởng mạnh đến variance. Nếu không xử lý hoặc loại bỏ các giá trị ngoại lai một cách thích hợp, kết quả từ variance có thể bị sai lệch và không phản ánh đúng tính chất của tập dữ liệu.
• Sử dụng không đúng trong trường hợp dữ liệu không đồng nhất: Phương sai là một phương pháp đo lường dựa trên giả định rằng dữ liệu được phân phối đồng nhất và có tính chất ngẫu nhiên. Trong trường hợp dữ liệu không đồng nhất hoặc không tuân theo phân phối chuẩn, việc sử dụng variance có thể không đưa ra kết quả chính xác và ảnh hưởng đến độ tin cậy của phân tích.

Để tránh những thách thức và rủi ro khi sử dụng phương sai, người sử dụng cần hiểu rõ về các giả định, giá trị đo lường, và tính chất của dữ liệu. Đồng thời, việc xử lý các giá trị ngoại lai và kiểm tra tính đồng nhất của dữ liệu sẽ giúp đảm bảo tính chính xác và hiệu quả khi sử dụng variance trong phân tích và quyết định.

Xem thêm: WACC là gi·: Khái niệm cơ bản và tác động đến quyết định tài chính

Như vậy, chúng ta đã cùng tìm hiểu variance là gì, chỉ số phương sai là một khái niệm quan trọng trong thống kê và tài chính, giúp đo lường mức độ biến đổi của dữ liệu trong một tập hợp. Việc hiểu rõ và ứng dụng phương sai một cách hợp lý trong các phân tích và quyết định kinh doanh là một yếu tố quan trọng để đạt được hiệu quả và thành công trong lĩnh vực này. Hẹn gặp lại các bạn trong các bài viết tiếp theo của góc nghề nghiệp nhé!